Hierarchical Reasoning Model

Guan Wang

^{1,\dagger}

, Jin Li

^{1}

, Yuhao Sun

^{1}

, Xing Chen

^{1}

, Changling Liu

^{1}

Yue Wu

^{1}

, Meng Lu

^{1,\dagger}

, Sen Song

^{2,\dagger}

, Yasin Abbasi Yadkori

^{1,\dagger}

^{1}

Sapient Intelligence, Singapore

^2

Tsinghua University

^{\dagger}

Corresponding author. Contact: [email protected].

Code available at: github.com/sapientinc/HRM

Abstract

Reasoning, the process of devising and executing complex goal-oriented action sequences, remains a critical challenge in AI. Current large language models (LLMs) primarily employ Chain-of-Thought (CoT) techniques, which suffer from brittle task decomposition, extensive data requirements, and high latency. Inspired by the hierarchical and multi-timescale processing in the human brain, we propose the Hierarchical Reasoning Model (HRM), a novel recurrent architecture that attains significant computational depth while maintaining both training stability and efficiency. HRM executes sequential reasoning tasks in a single forward pass without explicit supervision of the intermediate process, through two interdependent recurrent modules: a high-level module responsible for slow, abstract planning, and a low-level module handling rapid, detailed computations. With only 27 million parameters, HRM achieves exceptional performance on complex reasoning tasks using only 1000 training samples. The model operates without pre-training or CoT data, yet achieves nearly perfect performance on challenging tasks including complex Sudoku puzzles and optimal path finding in large mazes. Furthermore, HRM outperforms much larger models with significantly longer context windows on the Abstraction and Reasoning Corpus (ARC), a key benchmark for measuring artificial general intelligence capabilities. These results underscore HRM’s potential as a transformative advancement toward universal computation and general-purpose reasoning systems.

Figure 1: Left: HRM is inspired by hierarchical processing and temporal separation in the brain. It has two recurrent networks operating at different timescales to collaboratively solve tasks. Right: With only about 1000 training examples, the HRM (~27M parameters) surpasses state-of-the-art CoT models on inductive benchmarks (ARC-AGI) and challenging symbolic tree-search puzzles (Sudoku-Extreme, Maze-Hard) where CoT models failed completely. The HRM was randomly initialized, and it solved the tasks directly from inputs without chain of thoughts.

💭 Click to ask about this figure

1. Introduction

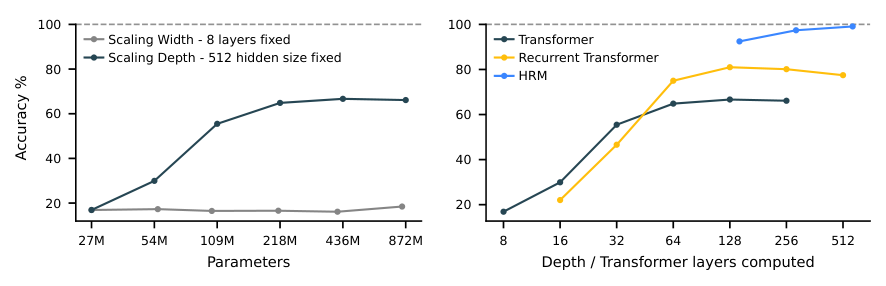
Deep learning, as its name suggests, emerged from the idea of stacking more layers to achieve increased representation power and improved performance [1,2]. However, despite the remarkable success of large language models, their core architecture is paradoxically shallow [3]. This imposes a fundamental constraint on their most sought-after capability: reasoning. The fixed depth of standard Transformers places them in computational complexity classes such as

AC^0

TC^0

[4], preventing them from solving problems that require polynomial time [5,6]. LLMs are not Turing-complete and thus they cannot, at least in a purely end-to-end manner, execute complex algorithmic reasoning that is necessary for deliberate planning or symbolic manipulation tasks [7,8]. For example, our results on the Sudoku task show that increasing Transformer model depth can improve performance,¹ but performance remains far from optimal even with very deep models (see Figure 2), which supports the conjectured limitations of the LLM scaling paradigm ([9]).

Simply increasing the model width does not improve performance here.

The LLMs literature has relied largely on Chain-of-Thought (CoT) prompting for reasoning [10]. CoT externalizes reasoning into token-level language by breaking down complex tasks into simpler intermediate steps, sequentially generating text using a shallow model [11]. However, CoT for reasoning is a crutch, not a satisfactory solution. It relies on brittle, human-defined decompositions where a single misstep or a misorder of the steps can derail the reasoning process entirely [12,13]. This dependency on explicit linguistic steps tethers reasoning to patterns at the token level. As a result, CoT reasoning often requires significant amount of training data and generates a large number of tokens for complex reasoning tasks, resulting in slow response times. A more efficient approach is needed to minimize these data requirements [14].

Towards this goal, we explore "latent reasoning", where the model conducts computations within its internal hidden state space [15,16]. This aligns with the understanding that language is a tool for human communication, not the substrate of thought itself [17]; the brain sustains lengthy, coherent chains of reasoning with remarkable efficiency in a latent space, without constant translation back to language. However, the power of latent reasoning is still fundamentally constrained by a model's effective computational depth. Naively stacking layers is notoriously difficult due to vanishing gradients, which plague training stability and effectiveness ([1,18]). Recurrent architectures, a natural alternative for sequential tasks, often suffer from early convergence, rendering subsequent computational steps inert, and rely on the biologically implausible, computationally expensive and memory intensive Backpropagation Through Time (BPTT) for training [19].

The human brain provides a compelling blueprint for achieving the effective computational depth that contemporary artificial models lack. It organizes computation hierarchically across cortical regions operating at different timescales, enabling deep, multi-stage reasoning ([20,21,22]). Recurrent feedback loops iteratively refine internal representations, allowing slow, higher-level areas to guide, and fast, lower-level circuits to execute—subordinate processing while preserving global coherence ([23,24,25]). Notably, the brain achieves such depth without incurring the prohibitive credit-assignment costs that typically hamper recurrent networks from backpropagation through time ([19,26]).

Inspired by this hierarchical and multi-timescale biological architecture, we propose the Hierarchical Reasoning Model (HRM). HRM is designed to significantly increase the effective computational depth. It features two coupled recurrent modules: a high-level (H) module for abstract, deliberate reasoning, and a low-level (L) module for fast, detailed computations. This structure avoids the rapid convergence of standard recurrent models through a process we term "hierarchical convergence." The slow-updating H-module advances only after the fast-updating L-module has completed multiple computational steps and reached a local equilibrium, at which point the L-module is reset to begin a new computational phase.

Furthermore, we propose a one-step gradient approximation for training HRM, which offers improved efficiency and eliminates the requirement for BPTT. This design maintains a constant memory footprint (

O(1)

compared to BPTT's

O(T)

for

T

timesteps) throughout the backpropagation process, making it scalable and more biologically plausible.

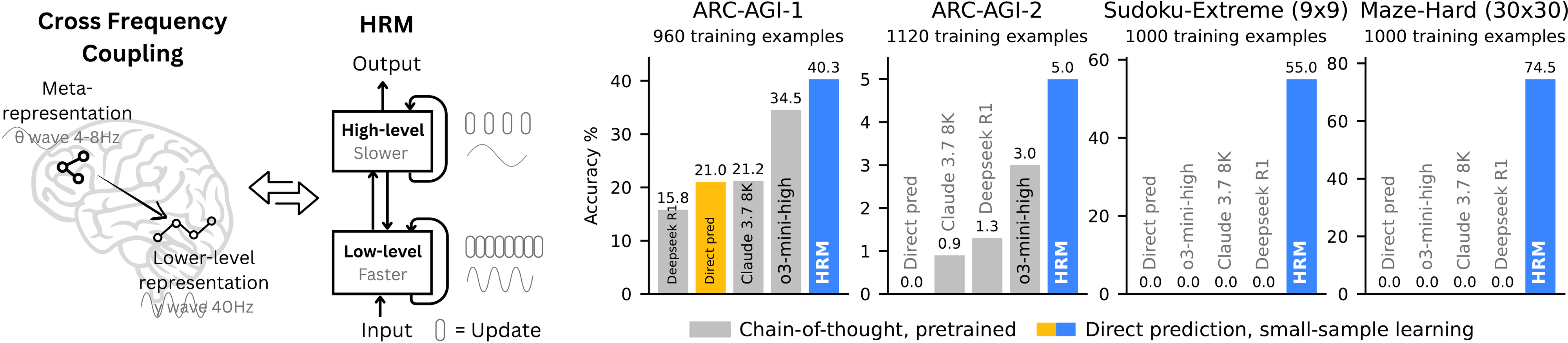
Leveraging its enhanced effective depth, HRM excels at tasks that demand extensive search and backtracking. Using only 1,000 input-output examples, without pre-training or CoT supervision, HRM learns to solve problems that are intractable for even the most advanced LLMs. For example, it achieves near-perfect accuracy in complex Sudoku puzzles (Sudoku-Extreme Full) and optimal pathfinding in 30x30 mazes, where state-of-the-art CoT methods completely fail (0% accuracy). In the Abstraction and Reasoning Corpus (ARC) AGI Challenge [27,28,29] - a benchmark of inductive reasoning - HRM, trained from scratch with only the official dataset (~1000 examples), with only 27M parameters and a 30x30 grid context (900 tokens), achieves a performance of 40.3%, which substantially surpasses leading CoT-based models like o3-mini-high (34.5%) and Claude 3.7 8K context (21.2%), despite their considerably larger parameter sizes and context lengths, as shown in Figure 1. This represents a promising direction toward the development of next-generation AI reasoning systems with universal computational capabilities.

2. Hierarchical Reasoning Model

We present the HRM, inspired by three fundamental principles of neural computation observed in the brain:

Hierarchical processing: The brain processes information across a hierarchy of cortical areas. Higher-level areas integrate information over longer timescales and form abstract representations, while lower-level areas handle more immediate, detailed sensory and motor processing ([20,22,21]).
Temporal Separation: These hierarchical levels in the brain operate at distinct intrinsic timescales, reflected in neural rhythms (e.g., slow theta waves, 4–8 Hz and fast gamma waves, 30–100 Hz) ([30,31]). This separation allows for stable, high-level guidance of rapid, low-level computations ([32,33]).
Recurrent Connectivity: The brain features extensive recurrent connections. These feedback loops enable iterative refinement, yielding more accurate and context-sensitive representations at the cost of additional processing time. Additionally, the brain largely avoids the problematic deep credit assignment problem associated with BPTT ([19]).

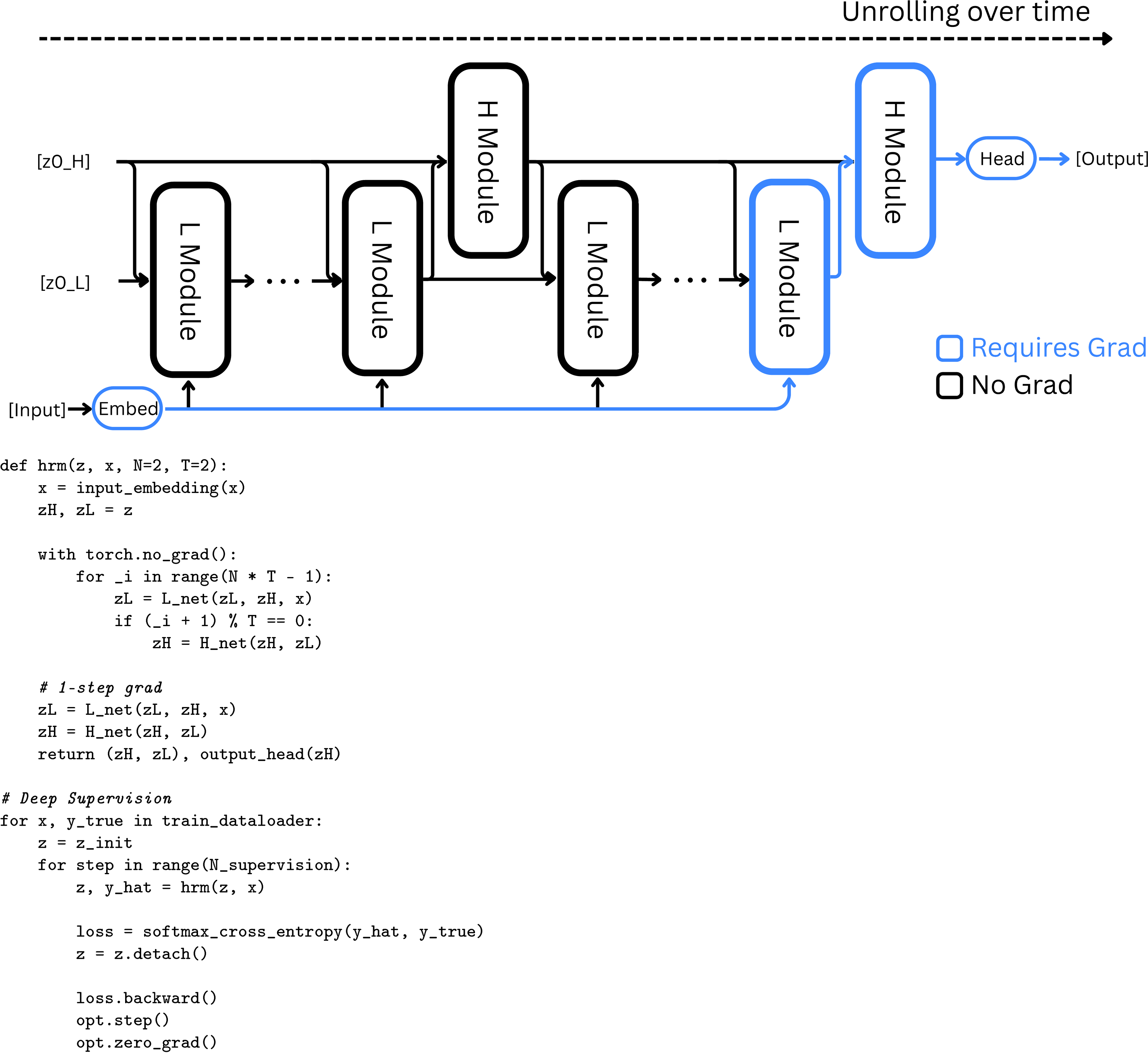
The HRM model consists of four learnable components: an input network

f_I(\cdot; \theta_I)

, a low-level recurrent module

f_L(\cdot; \theta_L)

, a high-level recurrent module

f_H(\cdot; \theta_H)

, and an output network

f_O(\cdot; \theta_O)

. The model's dynamics unfold over

N

high-level cycles of

T

low-level timesteps each². We index the total timesteps of one forward pass by

i = 1, \dots, N \times T

. The modules

f_L

and

f_H

each keep a hidden state---

z_L^i

for

f_L

and

z_H^i

for

f_H

---which are initialized with the vectors

z_L^0

and

z_H^0

, respectively.

While inspired by temporal separation in the brain, our model's "high-level" and "low-level" modules are conceptual abstractions and do not map directly to specific neural oscillation frequencies.

The HRM maps an input vector

x

to an output prediction vector

\hat{y}

as follows. First, the input

x

is projected into a working representation

\tilde{x}

by the input network:

At each timestep

i

, the L-module updates its state conditioned on its own previous state, the H-module’s current state (which remains fixed throughout the cycle), and the input representation. The H-module only updates once per cycle (i.e., every

T

timesteps) using the L-module’s final state at the end of that cycle:

\begin{align*} z_L^i &= f_L\left( z_L^{i-1}, z_H^{i-1}, \tilde{x}; \theta_L \right)\,, \\ z_H^i &= \begin{cases} f_H\left( z_H^{i-1}, z_L^{i-1}; \theta_H \right) & \text{if } i \equiv 0\ (\mathrm{mod}\ T)\,, \\ z_H^{i-1} & \text{otherwise }\;. \end{cases} \end{align*}

💭 Click to ask about this equation

Finally, after

N

full cycles, a prediction

\hat{y}

is extracted from the hidden state of the H-module:

This entire

NT

-timestep process represents a single forward pass of the HRM. A halting mechanism (detailed later in this section) determines whether the model should terminate, in which case

\hat{y}

will be used as the final prediction, or continue with an additional forward pass.

2.1.1.1 Hierarchical convergence

💭 Click to ask about this figure

Although convergence is crucial for recurrent networks, standard RNNs are fundamentally limited by their tendency to converge too early. As the hidden state settles toward a fixed point, update magnitudes shrink, effectively stalling subsequent computation and capping the network’s effective depth. To preserve computational power, we actually want convergence to proceed very slowly--but engineering that gradual approach is difficult, since pushing convergence too far edges the system toward instability.

HRM is explicitly designed to counteract this premature convergence through a process we term hierarchical convergence. During each cycle, the L-module (an RNN) exhibits stable convergence to a local equilibrium. This equilibrium, however, depends on the high-level state

z_H

supplied during that cycle. After completing the

T

steps, the H-module incorporates the sub-computation's outcome (the final state

z_L

) and performs its own update. This

z_H

update establishes a fresh context for the L-module, essentially "restarting" its computational path and initiating a new convergence phase toward a different local equilibrium.

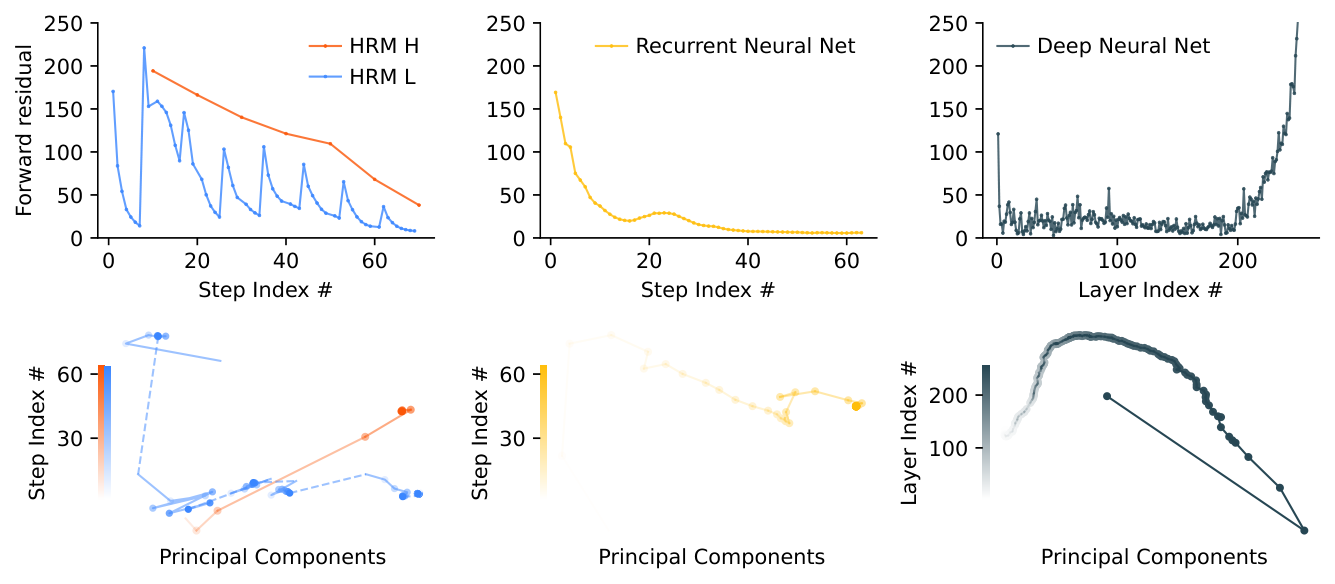
This process allows the HRM to perform a sequence of distinct, stable, nested computations, where the H-module directs the overall problem-solving strategy and the L-module executes the intensive search or refinement required for each step. Although a standard RNN may approach convergence within

T

iterations, the hierarchical convergence benefits from an enhanced effective depth of

NT

steps. As empirically shown in Figure 3, this mechanism allows HRM both to maintain high computational activity (forward residual) over many steps (in contrast to a standard RNN, whose activity rapidly decays) and to enjoy stable convergence. This translates into better performance at any computation depth, as illustrated in Figure 2.

2.1.1.2 Approximate gradient

Recurrent models typically use BPTT to compute gradients. However, BPTT requires storing the hidden states from the forward pass and then combining them with gradients during the backward pass, which demands

O(T)

memory for T timesteps. This heavy memory burden forces smaller batch sizes and leads to poor GPU utilization, especially for large-scale networks. Additionally, because retaining the full history trace through time is biologically implausible, it is unlikely that the brain implements BPTT [19].

Fortunately, if a recurrent neural network converges to a fixed point, we can avoid unrolling its state sequence by applying backpropagation in a single step at that equilibrium point. Moreover, such a mechanism could plausibly be implemented in the brain using only local learning rules [34,35]. Based on this finding, we propose a one-step approximation of the HRM gradient--using the gradient of the last state of each module and treating other states as constant. The gradient path is, therefore,

The above method needs

O(1)

memory, does not require unrolling through time, and can be easily implemented with an autograd framework such as PyTorch, as shown in Figure 4. Given that each module only needs to back-propagate errors through its most recent local synaptic activity, this approach aligns well with the perspective that cortical credit assignment relies on short-range, temporally local mechanisms rather than on a global replay of activity patterns.

The one-step gradient approximation is theoretically grounded in the mathematics of Deep Equilibrium Models (DEQ) ([36]) which employs the Implicit Function Theorem (IFT) to bypass BPTT, as detailed next. Consider an idealized HRM behavior where, during high-level cycle

k

, the L-module repeatedly updates until its state

z_L

converges to a local fixed point

z_L^\star

. This fixed point, given the current high-level state

z_H^{k-1}

, can be expressed as

The H-module then performs a single update using this converged L-state:

With a proper mapping

\mathcal{F}

, the updates to the high-level state can be written in a more compact form as

z_H^k = \mathcal{F}(z_H^{k-1}; \tilde{x}, \theta)

, where

\theta = (\theta_I, \theta_L)

, and the fixed-point can be written as

z_H^\star = \mathcal{F}(z_H^\star; \tilde{x}, \theta)

. Let

J_{\mathcal{F}} = \frac{\partial \mathcal{F}}{\partial z_H}

be the Jacobian of

\mathcal{F}

, and assume that the matrix

I - J_{\mathcal{F}}

is invertible at

z_H^\star

and that the mapping

\mathcal{F}

is continuously differentiable. The Implicit Function Theorem then allows us to calculate the exact gradient of fixed point

z_H^\star

with respect to the parameters

\theta

without explicit backpropagation:

Calculating the above gradient requires evaluating and inverting matrix

(I - J_{\mathcal{F}})

that can be computationally expensive. Given the Neumann series expansion,

the so-called 1-step gradient [37] approximates the series by considering only its first term, i.e.

(I - J_{\mathcal{F}})^{-1} \approx I

, and leads to the following approximation of Equation 1:

\frac{\partial z_H^*}{\partial\theta_H} \approx \frac{\partial f_H}{\partial \theta_H}, \quad \frac{\partial z_H^*}{\partial\theta_L}\approx \frac{\partial f_H}{\partial z^*_L} \cdot \frac{\partial z^*_L}{\partial \theta_L}, \quad \frac{\partial z_H^*}{\partial\theta_I} \approx \frac{\partial f_H}{\partial z^*_L} \cdot \frac{\partial z^*_L}{\partial \theta_I} \;.\tag{2}

💭 Click to ask about this equation

The gradients of the low-level fixed point,

\frac{\partial z^*_L}{\partial \theta_L}

and

\frac{\partial z^*_L}{\partial \theta_I}

, can also be approximated using another application of the 1-step gradient:

By substituting Equation 3 back into Equation 2, we arrive at the final simplified gradients.

Before defining our loss function, we must first introduce two key elements of our proposed method: deep supervision and adaptive computational time.

2.1.1.3 Deep supervision

Inspired by the principle that periodic neural oscillations regulate when learning occurs in the brain [38], we incorporate a deep supervision mechanism into HRM, as detailed next.

Given a data sample

(x, y)

, we run multiple forward passes of the HRM model, each of which we refer to as a segment. Let

M

denote the total number of segments executed before termination. For each segment

m \in \{1, \dots, M\}

, let

z^m = (z^{mNT}_H, z^{mNT}_L)

represent the hidden state at the conclusion of segment

m

, encompassing both high-level and low-level state components.

At each segment

m

, we apply a deep supervision step as follows:

Given the state $z^{m-1}$ from the previous segment, compute the next state $z^m$ and its associated output $\hat{y}^m$ through a forward pass in the HRM model:

Compute the loss for the current segment:

Update parameters:

The crucial aspect of this procedure is that the hidden state

z^m

is "detached" from the computation graph before being used as the input state for the next segment. Consequently, gradients from segment

m+1

do not propagate back through segment

m

, effectively creating a 1-step approximation of the gradient of the recursive deep supervision process ([39,40]). This approach provides more frequent feedback to the H-module and serves as a regularization mechanism, demonstrating superior empirical performance and enhanced stability in deep equilibrium models when compared to more complex, Jacobian-based regularization techniques ([39,41]). Figure 4 shows pseudocode of deep supervision training.

2.1.1.4 Adaptive computational time (ACT)

The brain dynamically alternates between automatic thinking ("System 1") and deliberate reasoning ("System 2") ([42]). Neuroscientific evidence shows that these cognitive modes share overlapping neural circuits, particularly within regions such as the prefrontal cortex and the default mode network ([43,44]). This indicates that the brain dynamically modulates the "runtime" of these circuits according to task complexity and potential rewards ([45,46]).

Inspired by the above mechanism, we incorporate an adaptive halting strategy into HRM that enables "thinking, fast and slow". This integration leverages deep supervision and uses the Q-learning algorithm [47] to adaptively determine the number of segments. A Q-head uses the final state of the H-module to predict the Q-values

\hat{Q}^m = (\hat{Q}^m_\text{halt}, \hat{Q}^m_\text{continue})

of the "halt" and "continue" actions:

where

\sigma

denotes the sigmoid function applied element-wise. The halt or continue action is chosen using a randomized strategy as detailed next. Let

M_{\max}

denote the maximum number of segments (a fixed hyperparameter) and

M_{\min}

denote the minimum number of segments (a random variable). The value of

M_{\min}

is determined stochastically: with probability

\varepsilon

, it is sampled uniformly from the set

\{2,\cdots,M_{\max}\}

(to encourage longer thinking), and with probability

1-\varepsilon

, it is set to 1. The halt action is selected under two conditions: when the segment count surpasses the maximum threshold

M_{\max}

, or when the estimated halt value

\hat{Q}_\text{halt}

exceeds the estimated continue value

\hat{Q}_\text{continue}

and the segment count has reached at least the minimum threshold

M_{\min}

The Q-head is updated through a Q-learning algorithm, which is defined on the following episodic Markov Decision Process (MDP). The state of the MDP at segment

m

z^m

, and the action space is

\{\text{halt}, \text{continue}\}

. Choosing the action "halt" terminates the episode and returns a binary reward indicating prediction correctness, i.e.,

\mathbf{1}\{\hat{y}^m = y\}

. Choosing "continue" yields a reward of 0 and the state transitions to

z^{m+1}

. Thus, the Q-learning targets for the two actions

\hat{G}^m = (\hat{G}^m_\text{halt}, \hat{G}^m_\text{continue})

are given by

\begin{align*} \hat{G}_\text{halt}^m &= \mathbf{1}\{\hat{y}^m = y\}\,, \\ \hat{G}_\text{continue}^m &= \begin{cases} \hat{Q}_\text{halt}^{m+1}, & \text{if $m \geq N_{\max}$}\,,\\[6pt] \max(\hat{Q}_\text{halt}^{m+1}, \hat{Q}_\text{continue}^{m+1})\,, & \text{otherwise}\;. \end{cases} \end{align*}

💭 Click to ask about this equation

We can now define the loss function of our learning procedure. The overall loss for each supervision segment combines both the Q-head loss and the sequence-to-sequence loss:

Minimizing the above loss enables both accurate predictions and nearly optimal stopping decisions.

Selecting the "halt" action ends the supervision loop. In practice, sequences are processed in batches, which can be easily handled by substituting any halted sample in the batch with a fresh sample from the dataloader.

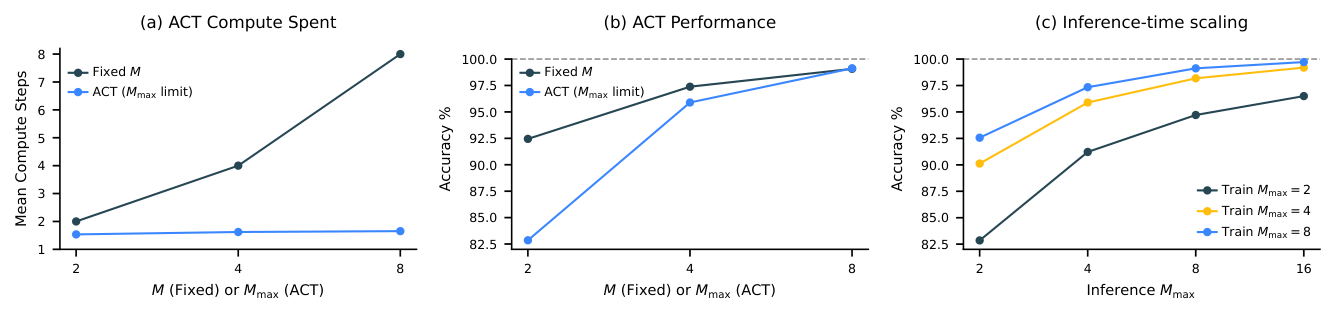
Figure 5 presents a performance comparison between two HRM variants: one incorporating ACT and another employing a fixed computational step count equivalent to ACT's

M_{\max}

parameter. It shows that ACT effectively adapts its computational resources based on task complexity, achieving significant computational savings with minimal impact on performance.

$Figure 5: **Effectiveness of Adaptive Computation Time (ACT)** on the *Sudoku-Extreme-Full*. **(a)** Mean compute steps used by models with ACT versus models with a fixed number of compute steps ($M$). ACT maintains a low and stable number of average compute steps even as the maximum limit ($M_{\max}$) increases. **(b)** Accuracy comparison. The ACT model achieves performance comparable to the fixed-compute model while utilizing substantially fewer computational steps on average. **(c)** Inference-time scalability. Models trained with a specific $M_{\max}$ can generalize to higher computational limits during inference, leading to improved accuracy. For example, a model trained with $M_{\max}=8$ continues to see accuracy gains when run with $M_{\max}=16$ during inference.$

Figure 5: Effectiveness of Adaptive Computation Time (ACT) on the Sudoku-Extreme-Full. (a) Mean compute steps used by models with ACT versus models with a fixed number of compute steps ( $M$ ). ACT maintains a low and stable number of average compute steps even as the maximum limit ( $M_{\max}$ ) increases. (b) Accuracy comparison. The ACT model achieves performance comparable to the fixed-compute model while utilizing substantially fewer computational steps on average. (c) Inference-time scalability. Models trained with a specific $M_{\max}$ can generalize to higher computational limits during inference, leading to improved accuracy. For example, a model trained with $M_{\max}=8$ continues to see accuracy gains when run with $M_{\max}=16$ during inference.

💭 Click to ask about this figure

2.1.1.5 Inference-time scaling

An effective neural model should exploit additional computational resources during inference to enhance performance. As illustrated in Figure 5-(c), HRM seamlessly achieves inference-time scaling by simply increasing the computational limit parameter,

M_{\max}

without requiring further training or architectural modifications.

Additional compute is especially effective for tasks that demand deeper reasoning. On Sudoku---a problem that often requires long-term planning---HRM exhibits strong inference-time scaling. On the other hand, we find that extra computational resources yield minimal gains in ARC-AGI challenge, as solutions generally require only a few transformations.

2.1.1.6 Stability of Q-learning in ACT

The deep Q-learning that underpins our ACT mechanism is known to be prone to instability, often requiring stabilization techniques such as replay buffers and target networks ([48]), which are absent in our design. Our approach, however, achieves stability through the intrinsic properties of our model and training procedure. Recent theoretical work by [49] shows that Q-learning can achieve convergence if network parameters are bounded, weight decay is incorporated during training, and post-normalization layers are implemented. Our model satisfies these conditions through its Post-Norm architecture that employs RMSNorm (a layer normalization variant) and the AdamW optimizer. AdamW has been shown to solve an

L_\infty

-constrained optimization problem, ensuring that model parameters remain bounded by

1/\lambda

([50]).

2.1.1.7 Architectural details

We employ a sequence-to-sequence architecture for HRM. Both input and output are represented as token sequences:

x = (x_1,\ldots,x_l)

and

y = (y_1,\ldots,y_{l^\prime})

respectively. The model includes an embedding layer

f_I

that converts discrete tokens into vector representations, and an output head

f_O(z; \theta_O) = \text{softmax}(\theta_O z)

that transforms hidden states into token probability distributions

\hat{y}

. For small-sample experiments, we replace softmax with stablemax [51] to improve generalization performance. The sequence-to-sequence loss is averaged over all tokens,

\text{L{\scriptsize OSS}}(\hat{y}, y) = \frac{1}{l^\prime} \sum_{i=1}^{l^\prime}\log p(y_i)

, where

p(y_i)

is the probability that distribution

\hat{y}_i

assigns to token

y_i

. The initial hidden states

z^0

are initialized by sampling from a truncated normal distribution with standard deviation of 1, truncation of 2, and kept fixed throughout training.

Both the low-level and high-level recurrent modules

f_L

and

f_H

are implemented using encoder-only Transformer [52] blocks with identical architectures and dimensions. These modules take multiple inputs, and we use straightforward element-wise addition to combine them, though more sophisticated merging techniques such as gating mechanisms could potentially improve performance and is left for future work. For all Transformer blocks in this work---including those in the baseline models---we incorporate the enhancements found in modern LLMs (based on Llama [53] architectures). These improvements include Rotary Positional Encoding ([54]), Gated Linear Units [55], RMSNorm [56], and the removal of bias terms from linear layers.

Furthermore, both HRM and recurrent Transformer models implement a Post-Norm architecture with weights initialized via truncated LeCun Normal initialization [57,58,59], while the scale and bias parameters are excluded from RMSNorm. All parameters are optimized using the Adam-atan2 optimizer ([60]), a scale-invariant variant of Adam ([61]), combined with a constant learning rate that includes linear warm-up.

3. Results

This section begins by describing the ARC-AGI, Sudoku, and Maze benchmarks, followed by an overview of the baseline models and their results. Figure 6-(a,b,c) presents a visual representation of the three benchmark tasks, which are selected to evaluate various reasoning abilities in AI models.

3.1 Benchmarks

ARC-AGI Challenge The ARC-AGI benchmark evaluates general fluid intelligence through IQ-test-like puzzles that require inductive reasoning [27]. The initial version, ARC-AGI-1, presents challenges as input-label grid pairs that force AI systems to extract and generalize abstract rules from just a few examples. Each task provides a few input–output demonstration pairs (usually 2–3) and a test input. An AI model has two attempts to produce the correct output grid. Although some believe that mastering ARC-AGI would signal true artificial general intelligence, its primary purpose is to expose the current roadblocks in AGI progress. In fact, both conventional deep learning methods and CoT techniques have faced significant challenges with ARC-AGI-1, primarily because it requires the ability to generalize to entirely new tasks ([28]).

Addressing the limitations identified in ARC-AGI-1, ARC-AGI-2 significantly expands the benchmark by providing a more comprehensive and carefully refined collection of tasks. These new tasks emphasize deeper compositional reasoning, multi-step logic, contextual rule application, and symbolic abstraction. Human calibration studies show these tasks are challenging but doable for people, while being much harder for current AI systems, offering a clearer measure of general reasoning abilities ([29]).

Sudoku-Extreme Sudoku is a 9

\times

9 logic puzzle, requiring each row, column, and 3

\times

3 block to contain the digits 1–9 exactly once. A prediction is considered correct if it exactly matches the puzzle's unique solution. Sudoku's complex logical structure makes it a popular benchmark for evaluating logical reasoning in machine learning ([62,63,64]).

The most frequently used Sudoku dataset in research, namely the Kaggle dataset ([65]), can be fully solved using elementary single-digit techniques ([66]). The minimal 17-clue puzzles ([62]), another widely-used collection, might seem more challenging due to its small number of clues. However, this perception is misleading---since 17 represents the minimum number of clues required to guarantee a unique Sudoku solution, these hints need to be highly orthogonal to each other. This orthogonal arrangement leads to many direct, easily-resolved solution paths [67].

We introduce Sudoku-Extreme, a more challenging dataset that is compiled from the aforementioned easy datasets as well as puzzles recognized by the Sudoku community as exceptionally difficult for human players:

Easy puzzles compiled from Kaggle, 17-clue, plus unbiased samples from the Sudoku puzzle distribution [67]: totaling 1149158 puzzles.
Challenging puzzles compiled from Magictour 1465, Forum-Hard and Forum-Extreme subsets: totaling 3104157 puzzles.

The compiled data then undergo a strict 90/10 train-test split, ensuring that the test set puzzles cannot be derived through equivalent transformations of any training samples. Sudoku-Extreme is a down-sampled subset of this data containing 1000 training examples. We use Sudoku-Extreme in our main experiments ( Figure 1), which focuses on small-sample learning scenarios. To guarantee convergence and control overfitting effects in our analysis experiments ( Figure 2, Figure 3, and Figure 5), we use the complete training data, Sudoku-Extreme-Full, containing 3831994 examples.

We measure puzzle difficulty by counting the number of search backtracks ("guesses") required by a smart Sudoku solver program tdoku, which uses propositional logic to reduce the number of guesses ([67]). Our Sudoku-Extreme dataset exhibits a mean difficulty of

22

backtracks per puzzle, significantly higher than existing datasets, including recent handmade puzzles Sudoku-Bench ([68]) which average just

0.45

backtracks per puzzle. These subset complexity levels are shown in Figure 6-(d).

Maze-Hard This task involves finding the optimal path in a 30

\times

30 maze, making it interpretable and frequently used for training LLMs in search tasks ([69,70,71]). We adopt the instance generation procedure of [71], but introduce an additional filter to retain only those instances whose difficulty exceeds 110. Here, "difficulty" is defined as the length of the shortest path, which aligns with the linear time complexity of the wavefront breadth-first search algorithm on GPUs ([72]). A path is considered correct if it is valid and optimal---that is, the shortest route from the start to the goal. The training and test set both include 1000 examples.

3.2 Evaluation Details

For all benchmarks, HRM models were initialized with random weights and trained in the sequence-to-sequence setup using the input-output pairs. The two-dimensional input and output grids were flattened and then padded to the maximum sequence length. The resulting performance is shown in Figure 1. Remarkably, HRM attains these results with just ~1000 training examples per task---and without pretraining or CoT labels.

For ARC-AGI challenge, we start with (1) all demonstration and test input-label pairs from the training set, and (2) all demonstration pairs along with test inputs from the evaluation set. The dataset is augmented by applying translations, rotations, flips, and color permutations to the puzzles. Each task example is prepended with a learnable special token that represents the puzzle it belongs to. At test time, we proceed as follows for each test input in the evaluation set: (1) Generate and solve 1000 augmented variants and, for each, apply the inverse‐augmentation transform to obtain a prediction. (2) Choose the two most popular predictions as the final outputs.³ All reported results are obtained by comparing the outputs with the withheld test labels from the evaluation set.

The ARC-AGI allows two attempts for each test input.

We augment Sudoku puzzles by applying band and digit permutations, while data augmentation is disabled for Maze tasks. Both tasks undergo only a single inference pass.

For ARC-AGI, the scores of the CoT models are taken from the official leaderboard ([29]), while for Sudoku and Maze, the scores are obtained by evaluating through the corresponding API.

In Figure 1, the baselines are grouped based on whether they are pre-trained and use CoT, or neither. The "Direct pred" baseline means using "direct prediction without CoT and pre-training", which retains the exact training setup of HRM but swaps in a Transformer architecture. Interestingly, on ARC-AGI-1, "Direct pred" matches the performance of [73], who built a carefully designed, domain-specific equivariant network for learning the ARC-AGI task from scratch, without pre-training. By substituting the Transformer architecture with HRM's hierarchical framework and implementing ACT, we achieve more than a twofold performance improvement.

On the Sudoku-Extreme and Maze-Hard benchmarks, the performance gap between HRM and the baseline methods is significant, as the baselines almost never manage to solve the tasks. These benchmarks that demand lengthy reasoning traces are particularly difficult for CoT-based methods. With only 1000 training examples, the "Direct pred" baseline---which employs an 8-layer Transformer identical in size to HRM---fails entirely on these challenging reasoning problems. When trained on the larger Sudoku-Extreme-Full dataset, however, "Direct pred" can solve some easy Sudoku puzzles and reaches

16.9\%

accuracy (see Figure 2). [71] showed that a large vanilla Transformer model with 175M parameters, trained on 1 million examples across multiple trials, achieved only marginal success on 30x30 Maze tasks, with accuracy below

20\%

using the

pass@64

evaluation metric.

3.3 Visualization of intermediate timesteps

Although HRM demonstrates strong performance on complex reasoning tasks, it raises an intriguing question: what underlying reasoning algorithms does the HRM neural network actually implement? Addressing this question is important for enhancing model interpretability and developing a deeper understanding of the HRM solution space.

While a definitive answer lies beyond our current scope, we begin our investigation by analyzing state trajectories and their corresponding solution evolution. More specifically, at each timestep

i

and given the low-level and high-level state pair (

z_L^i

and

z_H^i

) we perform a preliminary forward pass through the H-module to obtain

\bar{z}^{i} = f_H(z_H^i, z_L^i; \theta_H)

and its corresponding decoded prediction

\bar{y}^{i} = f_O(\bar{z}^{i}; \theta_O)

. The prediction

\bar{y}^{i}

is then visualized in Figure 7.

In the Maze task, HRM appears to initially explore several potential paths simultaneously, subsequently eliminating blocked or inefficient routes, then constructing a preliminary solution outline followed by multiple refinement iterations. In Sudoku, the strategy resembles a depth-first search approach, where the model appears to explore potential solutions and backtracks when it hits dead ends. HRM uses a different approach for ARC tasks, making incremental adjustments to the board and iteratively improving it until reaching a solution. Unlike Sudoku, which involves frequent backtracking, the ARC solution path follows a more consistent progression similar to hill-climbing optimization.

Importantly, the model shows that it can adapt to different reasoning approaches, likely choosing an effective strategy for each particular task. Further research is needed to gain more comprehensive insights into these solution strategies.

4. Brain Correspondence

$**Hierarchical Dimensionality Organization in the HRM and Mouse Cortex.** (a,b) are adapted from [74]. (a) Anatomical illustration of mouse cortical areas, color-coded by functional modules. (b) Correlation between Participation Ratio (PR), a measure of effective neural dimensionality, and hierarchical position across different mouse cortical areas. Higher positions in the hierarchy (e.g., MOs, ACAd) exhibit significantly higher PR values compared to lower sensory areas (e.g., SSp-n), with a Spearman correlation coefficient of $\rho$ = 0.79 (P = 0.0003). (c,d) **Trained HRM.** (c) PR scaling of the trained HRM with task diversity. The dimensionality of the high-level module ($z_H$) scales with the number of unique tasks (trajectories) included in the analysis, indicating an adaptive expansion of its representational capacity. In contrast, the low-level module's ($z_L$) dimensionality remains stable. (d) PR values for the low-level ($z_L$, PR = 30.22) and high-level ($z_H$, PR = 89.95) modules of the *trained* HRM, computed from neural activity during 100 unique Sudoku-solving trajectories. A clear dimensionality hierarchy is observed, with the high-level module operating in a substantially higher-dimensional space. (e,f) **Analysis of Untrained Network.** To verify that the dimensionality hierarchy is an emergent property of training, the same analyses were performed on an *untrained* HRM with random weights. (e) In contrast to the trained model's scaling in (c), the dimensionality of both modules in the untrained model remains low and stable, failing to scale with the number of tasks. (f) Similarly, contrasting with the clear separation in (d), the PR values for the untrained model's modules ($z_L$, PR = 42.09; $z_H$, PR = 40.75) are low and nearly identical, showing no evidence of hierarchical separation. This confirms that the observed hierarchical organization of dimensionality is a learned property that emerges through training, not an artifact of the model's architecture.$

Hierarchical Dimensionality Organization in the HRM and Mouse Cortex. (a,b) are adapted from [74]. (a) Anatomical illustration of mouse cortical areas, color-coded by functional modules. (b) Correlation between Participation Ratio (PR), a measure of effective neural dimensionality, and hierarchical position across different mouse cortical areas. Higher positions in the hierarchy (e.g., MOs, ACAd) exhibit significantly higher PR values compared to lower sensory areas (e.g., SSp-n), with a Spearman correlation coefficient of $\rho$ = 0.79 (P = 0.0003). (c,d) Trained HRM. (c) PR scaling of the trained HRM with task diversity. The dimensionality of the high-level module ( $z_H$ ) scales with the number of unique tasks (trajectories) included in the analysis, indicating an adaptive expansion of its representational capacity. In contrast, the low-level module's ( $z_L$ ) dimensionality remains stable. (d) PR values for the low-level ( $z_L$ , PR = 30.22) and high-level ( $z_H$ , PR = 89.95) modules of the trained HRM, computed from neural activity during 100 unique Sudoku-solving trajectories. A clear dimensionality hierarchy is observed, with the high-level module operating in a substantially higher-dimensional space. (e,f) Analysis of Untrained Network. To verify that the dimensionality hierarchy is an emergent property of training, the same analyses were performed on an untrained HRM with random weights. (e) In contrast to the trained model's scaling in (c), the dimensionality of both modules in the untrained model remains low and stable, failing to scale with the number of tasks. (f) Similarly, contrasting with the clear separation in (d), the PR values for the untrained model's modules ( $z_L$ , PR = 42.09; $z_H$ , PR = 40.75) are low and nearly identical, showing no evidence of hierarchical separation. This confirms that the observed hierarchical organization of dimensionality is a learned property that emerges through training, not an artifact of the model's architecture.

💭 Click to ask about this figure

A key principle from systems neuroscience is that a brain region's functional repertoire—its ability to handle diverse and complex tasks—is closely linked to the dimensionality of its neural representations ([75,76]). Higher-order cortical areas, responsible for complex reasoning and decision-making, must handle a wide variety of tasks, demanding more flexible and context-dependent processing ([77]). In dynamical systems, this flexibility is often realized through higher-dimensional state-space trajectories, which allow for a richer repertoire of potential computations ([78]). This principle gives rise to an observable dimensionality hierarchy, where a region's position in the processing hierarchy correlates with its effective dimensionality. To quantify this phenomenon, we can examine the Participation Ratio (PR), which serves as a standard measure of the effective dimensionality of a high-dimensional representation ([79]). The PR is calculated using the formula

where

\{\lambda_i\}

are the eigenvalues of the covariance matrix of neural trajectories. Intuitively, a higher PR value signifies that variance is distributed more evenly across many dimensions, corresponding to a higher-dimensional representation. Conversely, a lower PR value indicates that variance is concentrated in only a few principal components, reflecting a more compact, lower-dimensional structure.

The dimensionality hierarchy can be observed, for example, in the mouse cortex, where the PR of population activity increases monotonically from low-level sensory areas to high-level associative areas, supporting this link between dimensionality and functional complexity ([74]) ( Figure 8 (a,b)).

We evaluated whether HRM reproduces this neuroscientific principle by calculating the PR for both recurrent modules after training on the Sudoku-Extreme Full dataset. The PR computation used the covariance matrix derived from neural states gathered across multiple Sudoku-solving trajectories. The results show a striking parallel to the biological findings. The low-level module's state (

z_L

) occupies a relatively small subspace with a participation ratio of 30.22, whereas the high-level module's state (

z_H

) operates in a substantially larger subspace with a participation ratio of 89.95, as shown in Figure 8(c). Furthermore, Figure 8(d) shows that increasing the number of unique tasks (trajectories) from 10 to 100 causes

z_H

dimensionality to scale up accordingly, while

z_L

dimensionality remains stable. These results suggest an emergent separation of representational capacity between the modules that parallels their functional roles.

To confirm that this hierarchical organization is an emergent property of training, and not an artifact of the network's architecture, we performed a control analysis using an identical but untrained network with random weights.

We initialized an identical HRM architecture with random weights and, without any training, measured the PR of its modules as the network processed the same task-specific inputs given to the trained model.

The results, shown in Figure 8(e,f), reveal a stark contrast: the high-level and low-level modules of the untrained network exhibit no hierarchical separation, with their PR values remaining low and nearly indistinguishable from each other. This control analysis validates that the dimensionality hierarchy is an emergent property that arises as the model learns to perform complex reasoning.

The high-to-low PR ratio in HRM (

z_H/z_L \approx 2.98

) closely matches that measured in the mouse cortex (

\approx 2.25

). In contrast, conventional deep networks often exhibit neural collapse, where last-layer features converge to a low-dimensional subspace ([80,81,82]). HRM therefore departs from the collapse pattern and instead fosters a high-dimensional representation in its higher module. This is significant because such representations are considered crucial for cognitive flexibility and are a hallmark of higher-order brain regions like the prefrontal cortex (PFC), which is central to complex reasoning.

This structural parallel suggests the model has discovered a fundamental organizational principle. By learning to partition its representations into a high-capacity, high-dimensional subspace (

z_H

) and a more specialized, low-dimensional one (

z_L

), HRM autonomously discovers an organizational principle that is thought to be fundamental for achieving robust and flexible reasoning in biological systems. This provides a potential mechanistic explanation for the model's success on complex, long-horizon tasks that are intractable for models lacking such a differentiated internal structure. We emphasize, however, that this evidence is correlational. While a causal link could be tested via intervention (e.g., by constraining the H-module's dimensionality), such methods are difficult to interpret in deep learning due to potential confounding effects on the training process itself. Thus, the causal necessity of this emergent hierarchy remains an important question for future investigation.

5. Related Work

5.1.1.1 Reasoning and algorithm learning

Given the central role of reasoning problems and their close relation to algorithms, researchers have long explored neural architectures that enable algorithm learning from training instances. This line of work includes Neural Turing Machines (NTM) ([83]), the Differentiable Neural Computer (DNC) ([84]), and Neural GPUs ([85])--all of which construct iterative neural architectures that mimic computational hardware for algorithm execution, and are trained to learn algorithms from data. Another notable work in this area is Recurrent Relational Networks (RRN) [62], which executes algorithms on graph representations through graph neural networks.

Recent studies have integrated algorithm learning approaches with Transformer-based architectures. Universal Transformers extend the standard Transformer model by introducing a recurrent loop over the layers and implementing an adaptive halting mechanism. [86] demonstrate that looped Transformers can generalize to a larger number of recurrent steps during inference than what they were trained on. [16] propose adding continuous recurrent reasoning tokens to the Transformer. Finally, TransNAR [8] combine recurrent graph neural networks with language models.

Building on the success of CoT-based reasoning, a line of work have introduced fine-tuning methods that use reasoning paths from search algorithms (like A*) as SFT targets [87,71,70].

We also mention adaptive halting mechanisms designed to allocate additional computational resources to more challenging problems. This includes the Adaptive Computation Time (ACT) for RNNs [88] and follow-up research like PonderNet [89], which aims to improve the stability of this allocation process.

HRM further pushes the boundary of algorithm learning through a brain-inspired computational architecture that achieves exceptional data efficiency and model expressiveness, successfully discovering complex and diverse algorithms from just 1000 training examples.

5.1.1.2 Brain-inspired reasoning architectures

Developing a model with the reasoning power of the brain has long been a goal in brain-inspired computing. Spaun ([90]) is one notable example, which uses spiking neural networks to create distinct modules corresponding to brain regions like the visual cortex and prefrontal cortex. This design enables an architecture to perform a range of cognitive tasks, from memory recall to simple reasoning puzzles. However, its reasoning relies on hand-designed algorithms, which may limit its ability to learn new tasks. Another significant model is the Tolman-Eichenbaum Machine (TEM) ([91]), which is inspired by the hippocampal-entorhinal system's role in spatial and relational memory tasks. TEM proposes that medial entorhinal cells create a basis for structural knowledge, while hippocampal cells link this basis to sensory information. This allows TEM to generalize and explains the emergence of various cell types like grid, border, and place cells. Another approach involves neural sampling models ([92]), which view the neural signaling process as inference over a distribution, functioning similarly to a Boltzmann machine. These models often require hand-made rules to be set up for solving a specific reasoning task. In essence, while prior models are restricted to simple reasoning problems, HRM is designed to solve complex tasks that are hard for even advanced LLMs, without pre-training or task-specific manual design.

5.1.1.3 Hierarchical memory

The hierarchical multi-timescale structure also plays an important role in how the brain processes memory. Models such as Hierarchical Sequential Models [93] and Clockwork RNN [94] use multiple recurrent modules that operate at varying time scales to more effectively capture long-range dependencies within sequences, thereby mitigating the forgetting issue in RNNs.

Similar mechanisms have also been adopted in linear attention methods for memorizing long contexts (see the Discussions section). Since HRM focuses on reasoning, full attention is applied for simplicity. Incorporating hierarchical memory into HRM could be a promising future direction.

6. Discussions

6.1.1.1 Turing-completeness of HRM

Like earlier neural reasoning algorithms including the Universal Transformer ([95]), HRM is computationally universal when given sufficient memory and time constraints. In other words, it falls into the category of models that can simulate any Turing machine, overcoming the computational limitations of standard Transformers discussed previously in the introduction. Given that earlier neural algorithm reasoners were trained as recurrent neural networks, they suffer from premature convergence and memory intensive BPTT. Therefore, in practice, their effective computational depth remains limited, though still deeper than that of a standard Transformer. By resolving these two challenges and being equipped with adaptive computation, HRM could be trained on long reasoning processes, solve complex puzzles requiring intensive depth-first search and backtracking, and move closer to practical Turing-completeness.

6.1.1.2 Reinforcement learning with chain-of-thought

Beyond fine-tuning using human-annotated CoT, reinforcement learning (RL) represents another widely adopted training methodology. However, recent evidence suggests that RL primarily unlocks existing CoT-like capabilities rather than discovering fundamentally new reasoning mechanisms ([96,97,98,99]). Additionally, CoT-training with RL is known for its instability and data inefficiency, often requiring extensive exploration and careful reward design. In contrast, HRM takes feedback from dense gradient-based supervision rather than relying on a sparse reward signal. Moreover, HRM operates naturally in a continuous space, which is biologically plausible and avoids allocating same computational resources to each token, even though tokens vary in their reasoning and planning complexity [16].

6.1.1.3 Linear attention

Recurrence has been explored not only for its capability in universal computation, but also as a means to replace the attention mechanism in Transformers, which suffers from quadratic time and memory complexity ([100]). Recurrent alternatives offer a more efficient design by processing input tokens sequentially and predicting the next token at each time step, similar to early RNN-based language models.

Some linear-attention variants, such as Log-linear Attention [101], share an RNN-like state-update that can be interpreted as propagating multi-timescale summary statistics, thereby retaining long-range context without the quadratic memory growth of standard self-attention. However, substituting the attention mechanism alone does not change the fact that Transformers are still fixed-depth, and require CoT as a compensatory mechanism. Notably, linear attention can operate with a reduced key-value cache over extended contexts, making them more suitable for deployment on resource-constrained edge devices.

7. Conclusion

This work introduces the Hierarchical Reasoning Model, a brain-inspired architecture that leverages hierarchical structure and multi-timescale processing to achieve substantial computational depth without sacrificing training stability or efficiency. With only 27M parameters and training on just 1000 examples, HRM effectively solves challenging reasoning problems such as ARC, Sudoku, and complex maze navigation--tasks that typically pose significant difficulties for contemporary LLM and chain-of-thought models.

Although the brain relies heavily on hierarchical structures to enable most cognitive processes, these concepts have largely remained confined to academic literature rather than being translated into practical applications. The prevailing AI approach continues to favor non-hierarchical models. Our results challenge this established paradigm and suggest that the Hierarchical Reasoning Model represents a viable alternative to the currently dominant chain-of-thought reasoning methods, advancing toward a foundational framework capable of Turing-complete universal computation.

Acknowledgements We thank Mingli Yuan, Ahmed Murtadha Hasan Mahyoub and Hengshuai Yao for their insightful discussions and valuable feedback throughout the course of this work.

References

[1] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. MIT Press, 2016. http://www.deeplearningbook.org

[2] Kaiming He, X. Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 770–778, 2015.

[3] Lena Strobl. Average-hard attention transformers are constant-depth uniform threshold circuits, 2023.

[4] Tom Bylander. Complexity results for planning. In Proceedings of the 12th International Joint Conference on Artificial Intelligence - Volume 1, IJCAI'91, page 274–279, San Francisco, CA, USA, 1991. Morgan Kaufmann Publishers Inc. ISBN 1558601600.

[5] William Merrill and Ashish Sabharwal. A logic for expressing log-precision transformers. In Neural Information Processing Systems, 2023a.

[6] David Chiang. Transformers in DLOGTIME-uniform

\text{TC}^0

. Transactions on Machine Learning Research, 2025.

[7] Lucas Lehnert, Sainbayar Sukhbaatar, DiJia Su, Qinqing Zheng, Paul McVay, Michael Rabbat, and Yuandong Tian. Beyond a*: Better planning with transformers via search dynamics bootstrapping. In First Conference on Language Modeling, 2024a.

[8] Wilfried Bounsi, Borja Ibarz, Andrew Dudzik, Jessica B. Hamrick, Larisa Markeeva, Alex Vitvitskyi, Razvan Pascanu, and Petar Velivckovi'c. Transformers meet neural algorithmic reasoners. ArXiv, abs/2406.09308, 2024.

[9] William Merrill and Ashish Sabharwal. The parallelism tradeoff: Limitations of log-precision transformers. Transactions of the Association for Computational Linguistics, 11:531–545, 2023b. doi:10.1162/tacl_a_00562.

[10] Jason Wei, Yi Tay, et al. Chain-of-thought prompting elicits reasoning in large language models, 2022. arXiv preprint arXiv:2201.11903.

[11] William Merrill and Ashish Sabharwal. The expressive power of transformers with chain of thought. In ICLR, 2024.

[12] Xinyun Chen, Ryan A. Chi, Xuezhi Wang, and Denny Zhou. Premise order matters in reasoning with large language models. ArXiv, abs/2402.08939, 2024.

[13] Rongwu Xu, Zehan Qi, and Wei Xu. Preemptive answer "attacks" on chain-of-thought reasoning. In Annual Meeting of the Association for Computational Linguistics, 2024.

[14] Pablo Villalobos, Anson Ho, Jaime Sevilla, Tamay Besiroglu, Lennart Heim, and Marius Hobbhahn. Will we run out of data? limits of llm scaling based on human-generated data. arXiv preprint arXiv:2211.04325, 2022.

[15] Xinghao Chen, Anhao Zhao, Heming Xia, Xuan Lu, Hanlin Wang, Yanjun Chen, Wei Zhang, Jian Wang, Wenjie Li, and Xiaoyu Shen. Reasoning beyond language: A comprehensive survey on latent chain-of-thought reasoning, 2025.

[16] Xuan Shen, Yizhou Wang, Xiangxi Shi, Yanzhi Wang, Pu Zhao, and Jiuxiang Gu. Training large language models to reason in a continuous latent space. arXiv preprint arXiv:2412.07423, 2024.

[17] Evelina Fedorenko, Steven T Piantadosi, and Edward AF Gibson. Language is primarily a tool for communication rather than thought. Nature, 630(8017):575–586, 2024.

[18] Hongyu Wang, Shuming Ma, Li Dong, Shaohan Huang, Dongdong Zhang, and Furu Wei. Deepnet: Scaling transformers to 1,000 layers. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2024.

[19] Timothy P Lillicrap and Adam Santoro. Backpropagation through time and the brain. Current Opinion in Neurobiology, 55:82–89, 2019. ISSN 0959-4388. doi:https://doi.org/10.1016/j.conb.2019.01.011.

[20] John D Murray, Alberto Bernacchia, David J Freedman, Ranulfo Romo, Jonathan D Wallis, Xinying Cai, Camillo Padoa-Schioppa, Tatiana Pasternak, Hyojung Seo, Daeyeol Lee, et al. A hierarchy of intrinsic timescales across primate cortex. Nature neuroscience, 17(12):1661–1663, 2014.

[21] Roxana Zeraati, Yan-Liang Shi, Nicholas A Steinmetz, Marc A Gieselmann, Alexander Thiele, Tirin Moore, Anna Levina, and Tatiana A Engel. Intrinsic timescales in the visual cortex change with selective attention and reflect spatial connectivity. Nature communications, 14(1):1858, 2023.

[22] Julia M Huntenburg, Pierre-Louis Bazin, and Daniel S Margulies. Large-scale gradients in human cortical organization. Trends in cognitive sciences, 22(1):21–31, 2018.

[23] Victor AF Lamme and Pieter R Roelfsema. The distinct modes of vision offered by feedforward and recurrent processing. Trends in neurosciences, 23(11):571–579, 2000.

[24] Andre M Bastos, W Martin Usrey, Rick A Adams, George R Mangun, Pascal Fries, and Karl J Friston. Canonical microcircuits for predictive coding. Neuron, 76(4):695–711, 2012.

[25] Klara Kaleb, Barbara Feulner, Juan Gallego, and Claudia Clopath. Feedback control guides credit assignment in recurrent neural networks. Advances in Neural Information Processing Systems, 37:5122–5144, 2024.

[26] Timothy P Lillicrap, Adam Santoro, Luke Marris, Colin J Akerman, and Geoffrey Hinton. Backpropagation and the brain. Nature Reviews Neuroscience, 21(6):335–346, 2020.

[27] François Chollet. On the measure of intelligence (abstraction and reasoning corpus), 2019. arXiv preprint arXiv:1911.01547.

[28] Francois Chollet, Mike Knoop, Gregory Kamradt, and Bryan Landers. Arc prize 2024: Technical report. ArXiv, abs/2412.04604, 2024.

[29] Francois Chollet, Mike Knoop, Gregory Kamradt, Bryan Landers, and Henry Pinkard. Arc-agi-2: A new challenge for frontier ai reasoning systems. arXiv preprint arXiv:2505.11831, 2025.

[30] György Buzsáki. Gamma, alpha, delta, and theta oscillations govern cognitive processes. International Journal of Psychophysiology, 39:241–248, 2000.

[31] György Buzsáki. Rhythms of the Brain. Oxford university press, 2006.

[32] Anja Pahor and Norbert Jaušovec. Theta–gamma cross-frequency coupling relates to the level of human intelligence. Intelligence, 46:283–290, 2014.

[33] Adriano BL Tort, Robert W Komorowski, Joseph R Manns, Nancy J Kopell, and Howard Eichenbaum. Theta–gamma coupling increases during the learning of item–context associations. Proceedings of the National Academy of Sciences, 106(49):20942–20947, 2009.

[34] Benjamin Scellier and Yoshua Bengio. Equilibrium propagation: Bridging the gap between energy-based models and backpropagation. Frontiers in Computational Neuroscience, 11, 2016.

[35] Guillaume Bellec, Franz Scherr, Anand Subramoney, Elias Hajek, Darjan Salaj, Robert Legenstein, and Wolfgang Maass. A solution to the learning dilemma for recurrent networks of spiking neurons. Nature Communications, 11, 07 2020. doi:10.1038/s41467-020-17236-y.

[36] Shaojie Bai, J Zico Kolter, and Vladlen Koltun. Deep equilibrium models. In Advances in Neural Information Processing Systems, pages 690–701, 2019.

[37] Zhengyang Geng, Xinyu Zhang, Shaojie Bai, Yisen Wang, and Zhouchen Lin. On training implicit models. ArXiv, abs/2111.05177, 2021.

[38] Katarina Begus and Elizabeth Bonawitz. The rhythm of learning: Theta oscillations as an index of active learning in infancy. Developmental Cognitive Neuroscience, 45:100810, 2020. ISSN 1878-9293. doi:https://doi.org/10.1016/j.dcn.2020.100810.

[39] Shaojie Bai, Zhengyang Geng, Yash Savani, and J. Zico Kolter. Deep Equilibrium Optical Flow Estimation . In 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 610–620, 2022.

[40] Zaccharie Ramzi, Florian Mannel, Shaojie Bai, Jean-Luc Starck, Philippe Ciuciu, and Thomas Moreau. Shine: Sharing the inverse estimate from the forward pass for bi-level optimization and implicit models. ArXiv, abs/2106.00553, 2021.

[41] Shaojie Bai, Vladlen Koltun, and J. Zico Kolter. Stabilizing equilibrium models by jacobian regularization. In International Conference on Machine Learning, 2021.

[42] Daniel Kahneman and P Egan. Thinking, fast and slow (farrar, straus and giroux, new york), 2011.

[43] Matthew D Lieberman. Social cognitive neuroscience: a review of core processes. Annu. Rev. Psychol., 58(1):259–289, 2007.

[44] Randy L Buckner, Jessica R Andrews-Hanna, and Daniel L Schacter. The brain's default network: anatomy, function, and relevance to disease. Annals of the new York Academy of Sciences, 1124(1):1–38, 2008.

[45] Marcus E Raichle. The brain's default mode network. Annual review of neuroscience, 38(1):433–447, 2015.

[46] Andrew Westbrook and Todd S Braver. Cognitive effort: A neuroeconomic approach. Cognitive, Affective, & Behavioral Neuroscience, 15:395–415, 2015.

[47] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction. MIT Press, Cambridge, MA, 2018.

[48] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin A. Riedmiller. Playing atari with deep reinforcement learning. ArXiv, abs/1312.5602, 2013.

[49] Matteo Gallici, Mattie Fellows, Benjamin Ellis, Bartomeu Pou, Ivan Masmitja, Jakob Nicolaus Foerster, and Mario Martin. Simplifying deep temporal difference learning, 2025.

[50] Shuo Xie and Zhiyuan Li. Implicit bias of adamw: L inf norm constrained optimization. ArXiv, abs/2404.04454, 2024.

[51] Lucas Prieto, Melih Barsbey, Pedro A. M. Mediano, and Tolga Birdal. Grokking at the edge of numerical stability. In The Thirteenth International Conference on Learning Representations, 2025.

[52] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in neural information processing systems, pages 5998–6008, 2017.

[53] Meta AI. Llama 3: State-of-the-art open weight language models. Technical report, Meta, 2024. URL https://ai.meta.com/llama/

[54] Jianlin Su, Murtadha Ahmed, Yu Lu, Shengfeng Pan, Wen Bo, and Yunfeng Liu. Roformer: Enhanced transformer with rotary position embedding. Neurocomputing, 568:127063, 2024.

[55] Noam M. Shazeer. Glu variants improve transformer. ArXiv, abs/2002.05202, 2020.

[56] Biao Zhang and Rico Sennrich. Root mean square layer normalization. ArXiv, abs/1910.07467, 2019.

[57] Günter Klambauer, Thomas Unterthiner, Andreas Mayr, and Sepp Hochreiter. Self-normalizing neural networks. In Neural Information Processing Systems, 2017.

[58] JAX Developers. jax.nn.initializers.lecun_normal. Google Research, 2025. URL https://docs.jax.dev/en/latest/_autosummary/jax.nn.initializers.lecun_normal.html Accessed June 22, 2025.

[59] Yann LeCun, Léon Bottou, Genevieve B Orr, and Klaus-Robert Müller. Efficient backprop. In Neural networks: Tricks of the trade, pages 9–50. Springer, 2002.

[60] Katie E Everett, Lechao Xiao, Mitchell Wortsman, Alexander A Alemi, Roman Novak, Peter J Liu, Izzeddin Gur, Jascha Sohl-Dickstein, Leslie Pack Kaelbling, Jaehoon Lee, and Jeffrey Pennington. Scaling exponents across parameterizations and optimizers. In Forty-first International Conference on Machine Learning, 2024.

[61] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization, 2017.

[62] Rasmus Berg Palm, Ulrich Paquet, and Ole Winther. Recurrent relational networks. In Neural Information Processing Systems, 2017.

[63] Jieyi Long. Large language model guided tree-of-thought. ArXiv, abs/2305.08291, 2023.

[64] Yilun Du, Jiayuan Mao, and Josh Tenenbaum. Learning iterative reasoning through energy diffusion. ArXiv, abs/2406.11179, 2024.

[65] Kyubyong Park. Can convolutional neural networks crack sudoku puzzles? https://github.com/Kyubyong/sudoku 2018.

[66] Single-digit techniques. https://hodoku.sourceforge.net/en/tech_singles.php Accessed: 2025-06-16.

[67] Tom Dillion. Tdoku: A fast sudoku solver and generator. https://t-dillon.github.io/tdoku/ 2025.

[68] Jeffrey Seely, Yuki Imajuku, Tianyu Zhao, Edoardo Cetin, and Llion Jones. Sudoku-bench: Evaluating creative reasoning with sudoku variants. arXiv preprint arXiv:2505.16135, 2025.

[69] Luke Darlow, Ciaran Regan, Sebastian Risi, Jeffrey Seely, and Llion Jones. Continuous thought machines. arXiv preprint arXiv:2505.05522, 2025.

[70] DiJia Su, Sainbayar Sukhbaatar, Michael Rabbat, Yuandong Tian, and Qinqing Zheng. Dualformer: Controllable fast and slow thinking by learning with randomized reasoning traces, 2025.

[71] Lucas Lehnert, Sainbayar Sukhbaatar, DiJia Su, Qinqing Zheng, Paul McVay, Michael Rabbat, and Yuandong Tian. Beyond a*: Better planning with transformers via search dynamics bootstrapping. In First Conference on Language Modeling, 2024b.

[72] Mubbasir Kapadia, Francisco Garcia, Cory D. Boatright, and Norman I. Badler. Dynamic search on the gpu. In 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, pages 3332–3337, 2013. doi:10.1109/IROS.2013.6696830.

[73] Isaac Liao and Albert Gu. Arc-agi without pretraining, 2025. URL https://iliao2345.github.io/blog_posts/arc_agi_without_pretraining/arc_agi_without_pretraining.html

[74] Lorenzo Posani, Shuqi Wang, Samuel P Muscinelli, Liam Paninski, and Stefano Fusi. Rarely categorical, always high-dimensional: how the neural code changes along the cortical hierarchy. bioRxiv, pages 2024–11, 2025.

[75] Mattia Rigotti, Omri Barak, Melissa R. Warden, Xiao-Jing Wang, Nathaniel D. Daw, Earl K. Miller, and Stefano Fusi. The importance of mixed selectivity in complex cognitive tasks. Nature, 497:585–590, 2013. doi:10.1038/nature12160.

[76] Valerio Mante, David Sussillo, Krishna V. Shenoy, and William T. Newsome. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature, 503(7474):78–84, 2013. doi:10.1038/nature12742.

[77] Earl K. Miller and Jonathan D. Cohen. An integrative theory of prefrontal cortex function. Annual Review of Neuroscience, 24(1):167–202, 2001. doi:10.1146/annurev.neuro.24.1.167.

[78] Wolfgang Maass. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Computation, 14(11):2531–2560, 2002. doi:10.1162/089976602760407955.

[79] Ege Altan, Sara A. Solla, Lee E. Miller, and Eric J. Perreault. Estimating the dimensionality of the manifold underlying multi-electrode neural recordings. PLoS Computational Biology, 17(11):e1008591, 2021. doi:10.1371/journal.pcbi.1008591.

[80] Vardan Papyan, X. Y. Han, and David L. Donoho. Prevalence of neural collapse during the terminal phase of deep learning training. Proceedings of the National Academy of Sciences, 117(40):24652–24663, 2020. doi:10.1073/pnas.2015509117.

[81] Cong Fang, Hangfeng He, Qi Long, and Weijie J. Su. Exploring deep neural networks via layer–peeled model: Minority collapse in imbalanced training. Proceedings of the National Academy of Sciences, 118(43):e2103091118, 2021. doi:10.1073/pnas.2103091118.

[82] Zhihui Zhu, Tianyu Ding, Jinxin Zhou, Xiao Li, Chong You, Jeremias Sulam, and Qing Qu. A geometric analysis of neural collapse with unconstrained features. In Advances in Neural Information Processing Systems, volume 34 of NeurIPS, pages 29820–29834, 2021.

[83] Alex Graves, Greg Wayne, and Ivo Danihelka. Neural turing machines, 2014.

[84] Alex Graves, Greg Wayne, Malcolm Reynolds, Tim Harley, Ivo Danihelka, Agnieszka Grabska-Barwińska, Sergio Gómez Colmenarejo, Edward Grefenstette, Tiago Ramalho, John Agapiou, et al. Hybrid computing using a neural network with dynamic external memory. Nature, 538(7626):471–476, 2016.

[85] Lukasz Kaiser and Ilya Sutskever. Neural GPUs learn algorithms. In ICLR, 2016.

[86] Jonas Geiping, Sean McLeish, Neel Jain, John Kirchenbauer, Siddharth Singh, Brian R. Bartoldson, Bhavya Kailkhura, Abhinav Bhatele, and Tom Goldstein. Scaling up test-time compute with latent reasoning: A recurrent depth approach, 2025.

[87] Tiedong Liu and Kian Hsiang Low. Goat: Fine-tuned llama outperforms gpt-4 on arithmetic tasks. ArXiv, abs/2305.14201, 2023.

[88] Alex Graves. Adaptive computation time for recurrent neural networks. ArXiv, abs/1603.08983, 2016.

[89] Andrea Banino, Jan Balaguer, and Charles Blundell. Pondernet: Learning to ponder. ArXiv, abs/2107.05407, 2021.

[90] Chris Eliasmith, Terrence C Stewart, Xuan Choo, Trevor Bekolay, Travis DeWolf, Yichuan Tang, and Daniel Rasmussen. A large-scale model of the functioning brain. science, 338(6111):1202–1205, 2012.

[91] James CR Whittington, Timothy H Muller, Shirley Mark, Guifen Chen, Caswell Barry, Neil Burgess, and Timothy EJ Behrens. The tolman-eichenbaum machine: unifying space and relational memory through generalization in the hippocampal formation. Cell, 183(5):1249–1263, 2020.

[92] Lars Buesing, Johannes Bill, Bernhard Nessler, and Wolfgang Maass. Neural dynamics as sampling: a model for stochastic computation in recurrent networks of spiking neurons. PLoS computational biology, 7(11):e1002211, 2011.

[93] Salah Hihi and Yoshua Bengio. Hierarchical recurrent neural networks for long-term dependencies. In D. Touretzky, M.C. Mozer, and M. Hasselmo, editors, Advances in Neural Information Processing Systems, volume 8. MIT Press, 1995.

[94] Jan Koutník, Klaus Greff, Faustino J. Gomez, and Jürgen Schmidhuber. A clockwork rnn. In International Conference on Machine Learning, 2014.

[95] Mostafa Dehghani, Stephan Gouws, Oriol Vinyals, Jakob Uszkoreit, and Lukasz Kaiser. Universal transformers, 2018. arXiv preprint arXiv:1807.03819.

[96] Yiping Wang, Qing Yang, Zhiyuan Zeng, Liliang Ren, Lucas Liu, Baolin Peng, Hao Cheng, Xuehai He, Kuan Wang, Jianfeng Gao, Weizhu Chen, Shuohang Wang, Simon Shaolei Du, and Yelong Shen. Reinforcement learning for reasoning in large language models with one training example, 2025. URL https://arxiv.org/abs/2504.20571

[97] Niklas Muennighoff. s1: Simple test-time scaling. arXiv preprint arXiv:2502.23456, 2025.

[98] Liang Wen, Yunke Cai, Fenrui Xiao, Xin He, Qi An, Zhenyu Duan, Yimin Du, Junchen Liu, Lifu Tang, Xiaowei Lv, Haosheng Zou, Yongchao Deng, Shousheng Jia, and Xiangzheng Zhang. Light-r1: Curriculum sft, dpo and rl for long cot from scratch and beyond, 2025.

[99] Xuefeng Li, Haoyang Zou, and Pengfei Liu. Limr: Less is more for rl scaling, 2025.

[100] Tri Dao and Albert Gu. Transformers are ssms: Generalized models and efficient algorithms through structured state space duality. ArXiv, abs/2405.21060, 2024.

[101] Han Guo, Songlin Yang, Tarushii Goel, Eric P Xing, Tri Dao, and Yoon Kim. Log-linear attention. arXiv preprint arXiv:2506.04761, 2025.